Omnidirectional_Wheel_Dynamics_Modeling/Omnidirectional Wheel Dynamics Modeling.md

全向轮整车动力学建模

本模型假设各轮子与地面摩擦力一致且不会打滑，机体一定与地面水平。理论上能够通过力控3508实现对车辆速度控制，一定程度上避免速度环PID控制调参不够完美带来的四轮运动不统一问题。

1.1模型定义

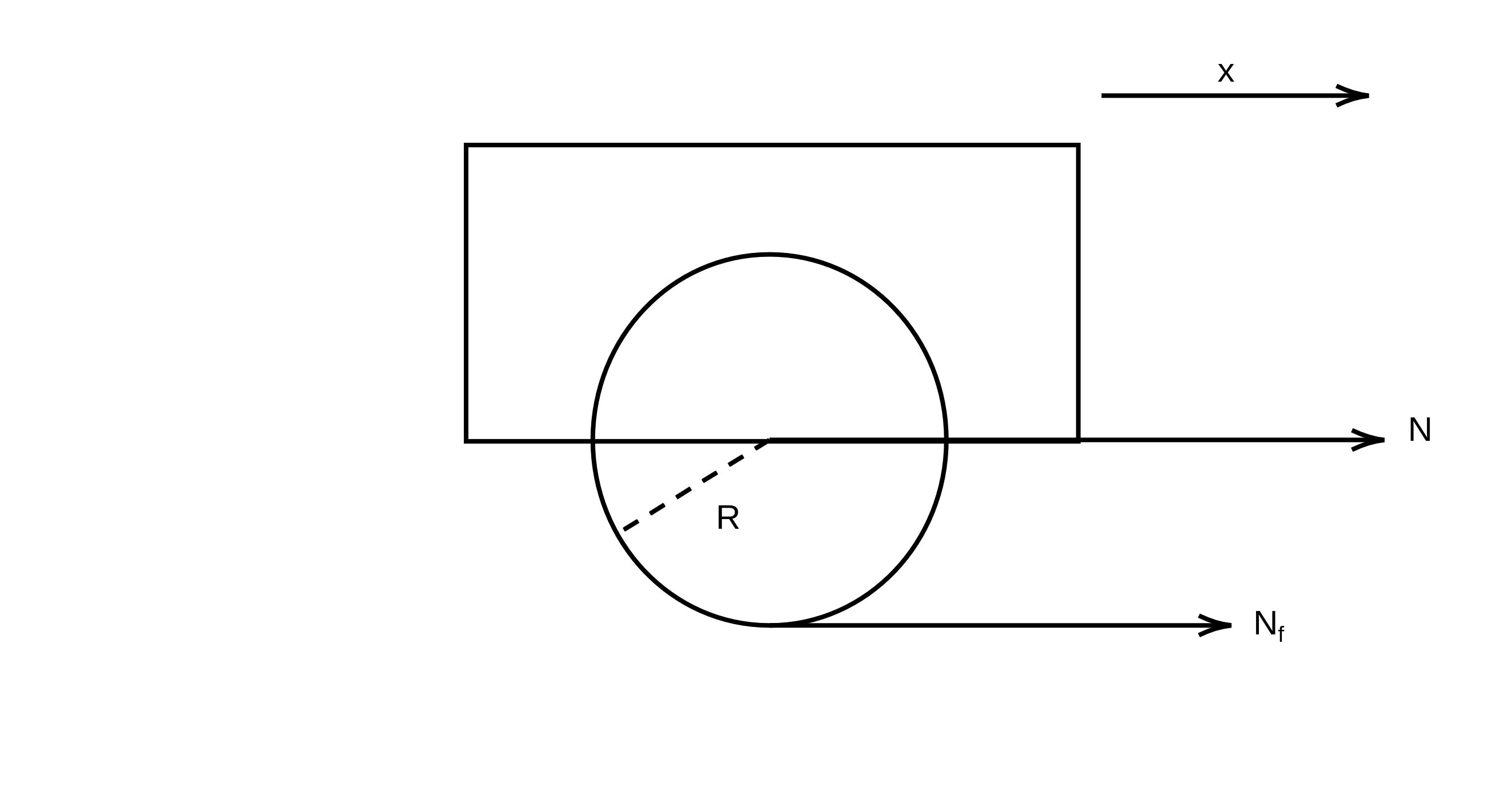
首先仅考虑x方向移动，机器人抽象为方形机体和圆形驱动轮。假设有神秘力量保证机体一定水平。

变量与参数定义如下表所示

符号	含义	正方向	单位
x	机体位移	箭头所示	m
N	驱动轮对机体的力	箭头所示	N
N_f	地面对驱动轮摩擦力	箭头所示	N
F_x	虚拟的驱动轮输出力	方向同x	N
T	驱动轮输出力矩	方向同x	N·m
\omega	绕质心转动角速度	逆时针	rad/s

符号	含义	单位
m	驱动轮转子质量	kg
M	机体质量	kg
I_w	驱动轮转资转动惯量	kg·m^2
I	机体绕质心转动惯量	kg·m^2

1.2经典力学分析

首先只考虑x方向移动

对驱动轮：

 m\ddot{x}=N_f-N  \tag{1}

I\frac{\ddot{x}}{R}=T-N_fR  \tag{2}

合并上两式子，消去N_f得：

\ddot{x} = \frac{T-NR}{\frac{I_w}{R}+mR} \tag{3}

对机体：

N=M\ddot{x}\tag{4}

（3），（4）式子可求得：

\ddot{x} = \frac{1}{\frac{I_w}{R}+(m+M)R}T \tag{5}

（5）看作 \ddot{x} 关于 T 的函数两侧积分：

\dot{x} = \frac{1}{2}\frac{1}{\frac{I_w}{R}+(m+M)R}T^2 \tag{6}

设虚拟力：

F_x = \frac{T}{R}\tag{7}

（7）带入（6）得：

\dot{x} = \frac{1}{2}\frac{R^2}{\frac{I_w}{R}+(m+M)R}F_x^2 \tag{6}

得到x方向上速度与驱动轮输出力的关系，同理可得y方向上的表达式，参考全向轮速度分解，到每个轮子电机的输出力上。

旋转：

F_{yaw} = I\frac{\omega}{L}

其中L为轮子转轴中心到车辆转轴中心水平距离。

再将 F_{yaw} 也叠加到各个电机输出上即可。

由于电机输出力矩与电流正相关，即可实现力控。具体结果公式参见手稿。